Notion de spectre

Le spectre est une représentation de l’amplitude du signal sonore en fonction de la fréquence. Dans le cas d’un signal périodique (figure du haut ci-dessous), il est constitué d’une série de pics régulièrement espacés entre eux (figure du bas ci-dessous).

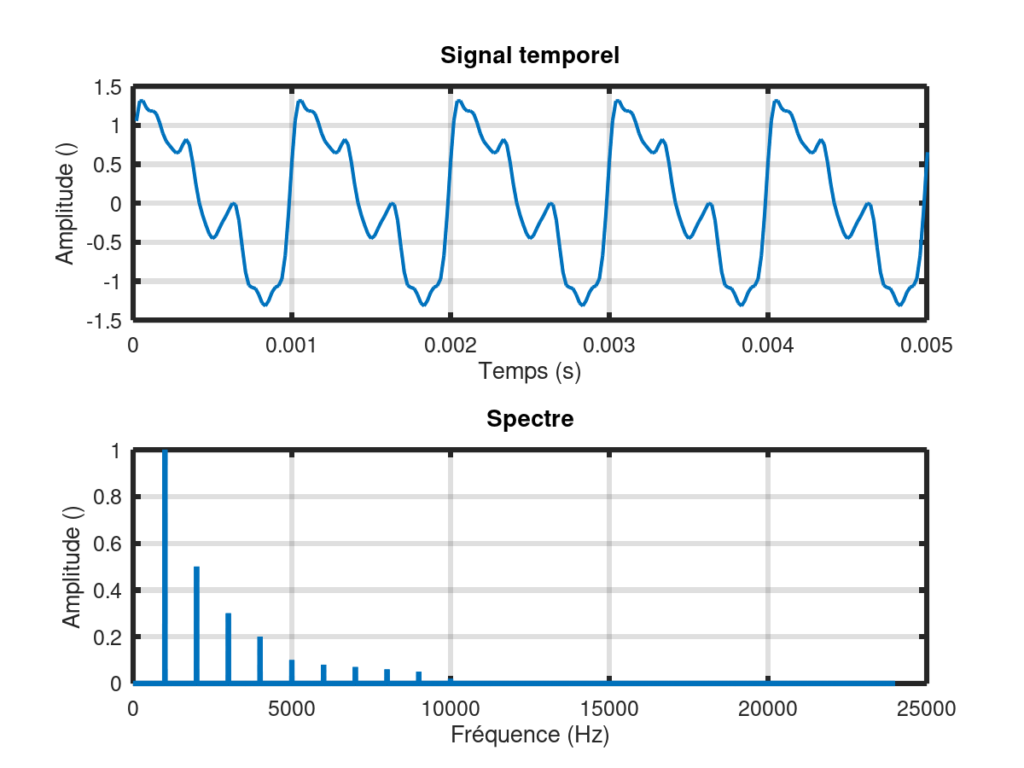
Fréquence fondamentale

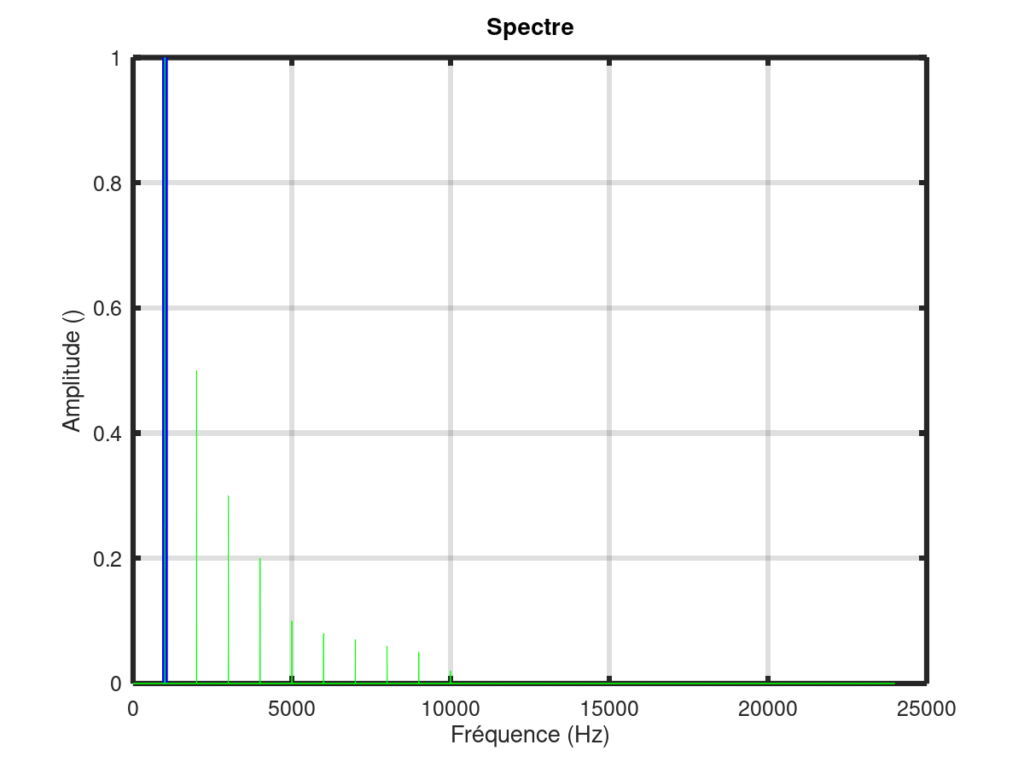
La fréquence fondamentale est définie comme l’inverse de la période du signal. Elle apparaît sur le spectre au niveau du premier pic (pic bleu sur la figure ci-dessous).

Harmoniques

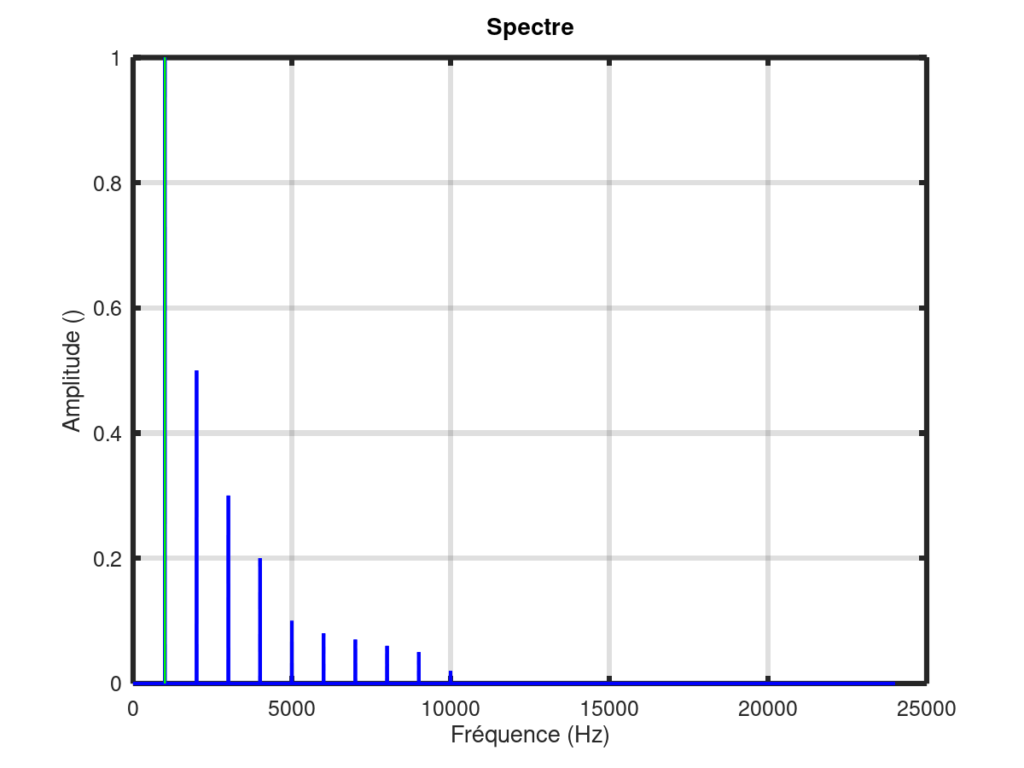
Les harmoniques sont les composantes dont les fréquences sont les multiples entières de la fréquence fondamentale f_0 : 2 f_0, 3 f_0, 4 f_0, .... Les harmoniques sont représentés en bleu sur la figure ci-dessous (la fréquence fondamentale en vert).

Notion de timbre

Le timbre est défini (en partie) par le nombre et l’amplitude relative des harmoniques dans un signal. Dans la figure ci-dessous les deux sons ont la même fréquence fondamentale (200 Hz) mais les spectres sont clairement différents

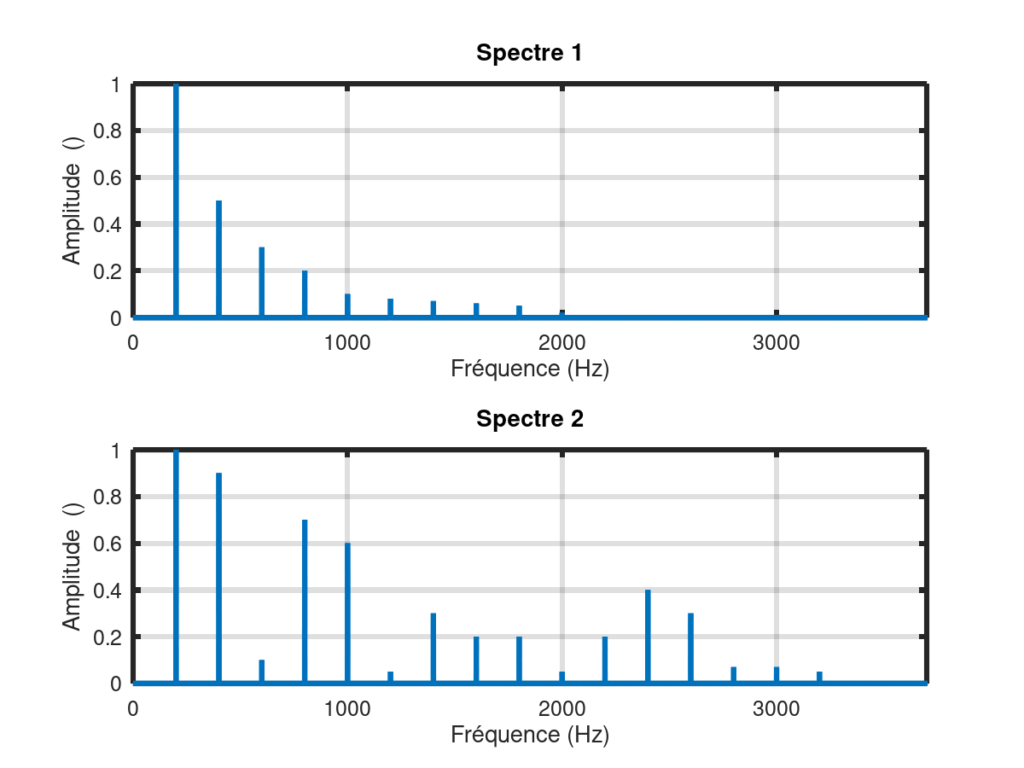
Le son 2 (spectre 2) est plus riche que le son 1 (spectre 1), comme on peut l’entendre ci-dessous.

Harmoniques pairs ou impairs?

Un signal carré n’émet que des harmoniques impairs et la clarinette a la particularité d’émettre principalement des harmoniques impairs (notamment si on écoutait le signal présent dans le bec).

Partiels

Si un son contient des partiels, cela signifie que les fréquences différentes de la fréquence fondamentale ne sont pas des multiples entiers de la fréquence fondamentale. Par exemple, si f_0 les fréquences des partiels peuvent être 1.8 f_0, 3.1 f_0, 3;9 f_0, 5.2 f_0... . Dans ce cas le spectre ne montre pas de pics régulièrement espacés entre eux (cf. figure ci-dessous).

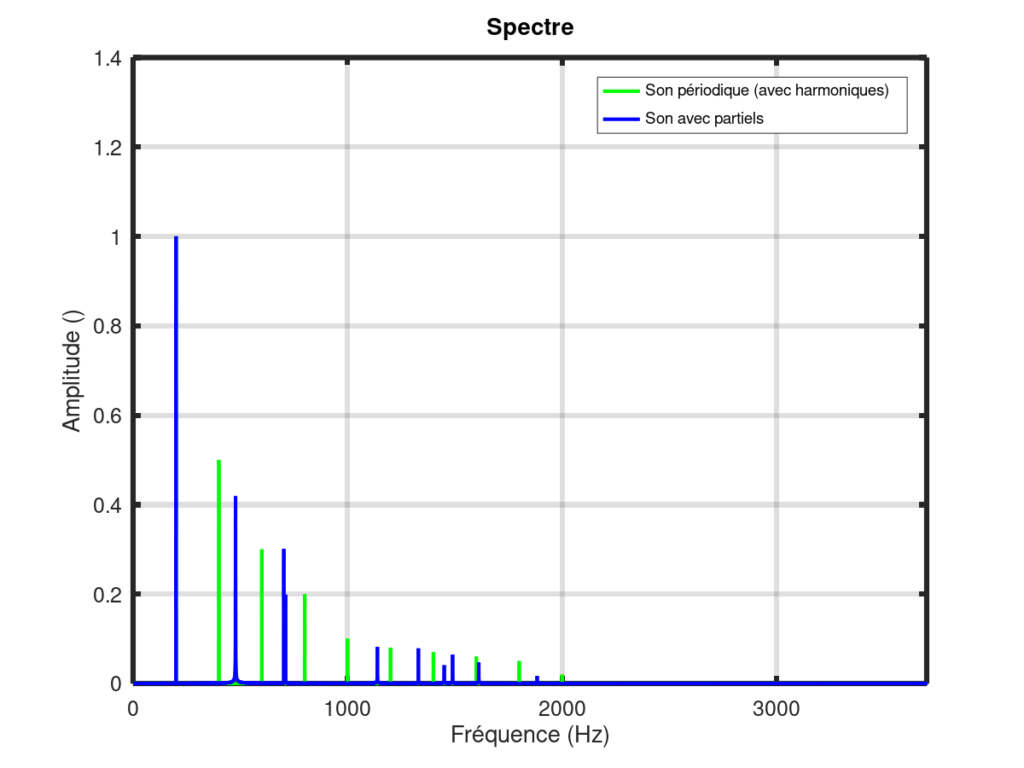
Un exemple sonore de son contenant des partiels est donné ci-dessous. Les partiels créent des phénomènes de battements (modification de l’amplitude du son en fonction du temps).